Fixing Boundary Violations: Applying Constrained
Optimization to the Truncated Regression Model
2.3 Type II Boundary Constraints
Type II constraints are related to the regression coefficient $\beta$, which is best
illustrated by the centered model
\begin{equation*}
{{y}_{i}}=\boldsymbol{x_{i}^{*}\beta},
\end{equation*}
where $\boldsymbol{{x}^{*}}$ refers to the matrix of the independent variables $\boldsymbol{x_{j}}$,
$j=1,\ldots ,m$, after being centered at the means ${{\bar{x}}_{j}}$,
\begin{equation*}
\boldsymbol{x^{*}}=\left(
\begin{matrix}
\vdots & \vdots & & \vdots \\
1 & \left( {{x}_{1i}}-{{\bar{x}}_{1}} \right) & \cdots & \left( {{x}_{mi}}-{{\bar{x}}_{m}} \right)\\
\vdots & \vdots & & \vdots
\end{matrix}
\right).
\end{equation*}
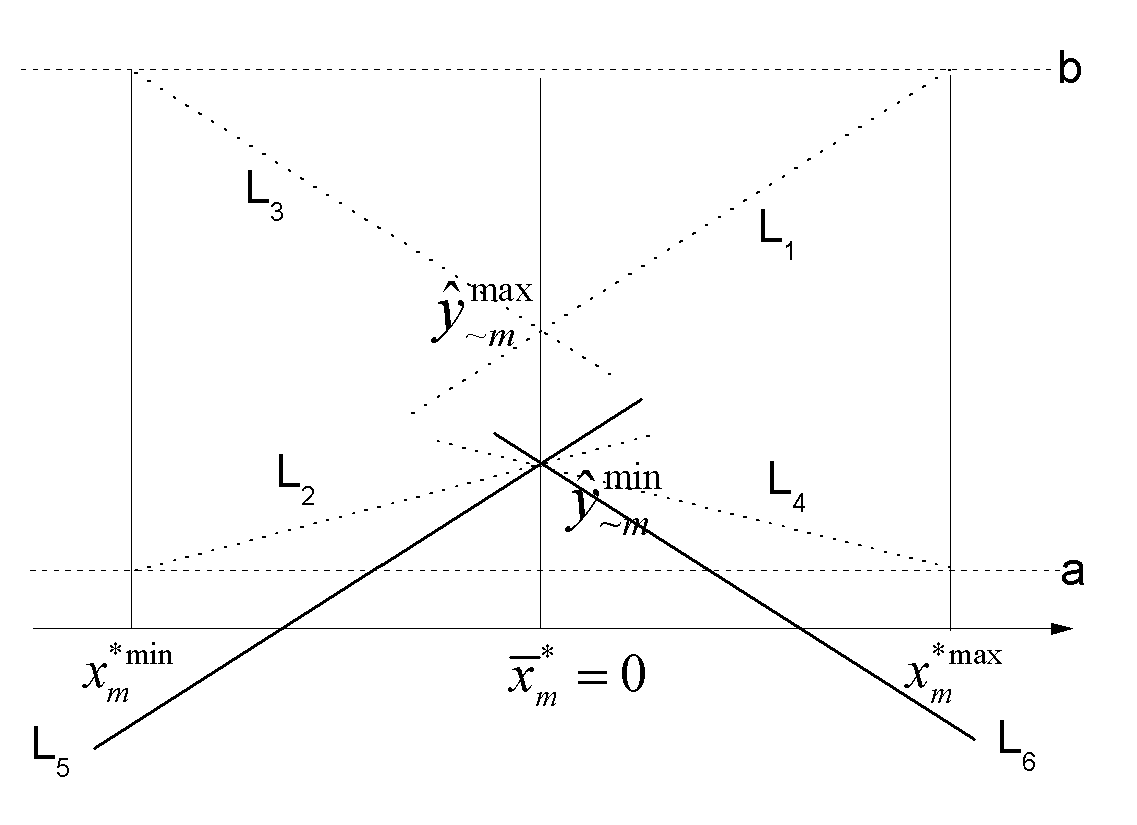
Figure 1 Boundary Constraints of $\beta_{m}$
The constant ${{\hat{\beta }}_{0}}$ now represents the mean estimate of $y_{i}$ when none
of the covariates has explanatory power, or represents the baseline predicted value of $y_{i}$ when all covariates
are held by the means. Apparently, the boundary constraints of ${{\hat{\beta }}_{0}}$ should be within the truncation
interval
\begin{equation*}
a\le {{\hat{\beta }}_{0}}\le b.
\end{equation*}
To discover the possible range of other ${{\hat{\beta }}_{m}}$, we first hold ${{x}_{m}^{*}}$ at the mean
level $\bar{x}_{m}^{*}$ as Figure 1 shows, and then derive the maximum and minimum of the predicted values,
$\hat{y}_{\sim m}^{\max }$ and $\hat{y}_{\sim m}^{\min }$, respectively. The notation "$\sim$$m$"
represents the fact that ${{x}_{m}^{*}}$ has no contribution when it is held at the mean. More precisely,
$\hat{y}_{\sim m}^{\max }$ and $\hat{y}_{\sim m}^{\min }$ can be specified
\begin{align*}
&\hat{y}_{\sim m}^{\max}=\sum\limits_{j=0,j\ne m}{\left(v_{j}^{+}
{{\hat{\beta}}_{j}}x_{j}^{*\max}+v_{j}^{-}{{\hat{\beta}}_{j}}x_{j}^{*\min} \right)} \\
&\hat{y}_{\sim m}^{\min}=\sum\limits_{j=0,j\ne m}{\left(v_{j}^{+}{{\hat{\beta}}_{j}}x_{j}^{*\min}+v_{j}^{-}
{{\hat{\beta}}_{j}}x_{j}^{*\max} \right)}.
\end{align*}
The upper limit of $\beta_{m}$ is the flatter positive slope of the line $L_{1}$ or $L_{2}$.
The lower limit is the flatter negative slope of the line $L_{3}$ or $L_{4}$. Therefore, the boundary
constraints of ${{\hat{\beta }}_{m}}$ can be identified as
\begin{equation*}
\max \left( \frac{a-\hat{y}_{\sim m}^{\min }}{x_{m}^{*\max }},-\frac{\hat{y}_{\sim m}^{\max }-b}
{x_{m}^{*\min }} \right)\le {{\hat{\beta }}_{m}}\le \min \left( \frac{b-\hat{y}_{\sim m}^{\max }}
{x_{m}^{*\max }},-\frac{\hat{y}_{\sim m}^{\min }-a}{x_{m}^{*\min }} \right).
\end{equation*}
If $\hat{\beta}_{m}$ takes the steeper slope, such as $L_{5}$ or $L_{6}$ shows, it would generate
an out-of-bounds predicted value when we vary ${{x}_{m}^{*}}$ from the mean to the maximum or minimum,
holding other variables at the baseline level. In this sense, a type II violation can always be
translated into a type I violation.
Different centering methods do not generate different estimates of the beta coefficients, except the constant, which is a linear combination of all other beta coefficients and the centered covariate values.7 For a truncated regression model with $m$ covariates, there will always be $(2m+2)$ type II boundary constraints, including the constant.
____________________
Footnote
7 This rule only applies to a strict linear model. If truncated regression is specified with a nonlinear relationship, such as interaction, different centering methods will generate different results.
